Bezier Curve Pratice

贝塞尔曲线被广泛地在计算机图形中用来为平滑曲线建立模型,下面是一个三元的示例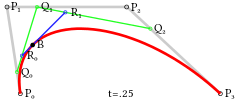

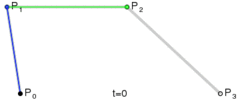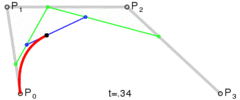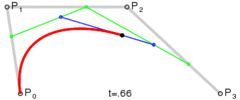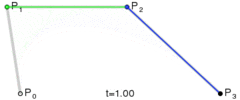
贝赛尔曲线都可以理解为由给定点P0、P1、P2的函数B(t)追踪,对于一维的贝赛尔曲线来说,就是一条直线

• 线性贝塞尔曲线

  给定点P0、P1，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出:

  \[\mathbf{B}(t)=\mathbf{P}_0 + (\mathbf{P}_1-\mathbf{P}_0)t=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1]\]

private float getInterpolatorDistance(float input) {
    return (1 - input) * p0 + input * p1;
}

• 二次方贝塞尔曲线

  路径由给定点P0、P1、P2的函数B（t）追踪:

  \[\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } t \in [0,1]\]

Alice->Bob: hello,Bob.
Note right of Bob: Bob thinks.
Bob->Alice: Thanks